Двоичная система счисления

Откройте рисунок "Алгоритм перевода чисел из десятичной системы в двоичную".

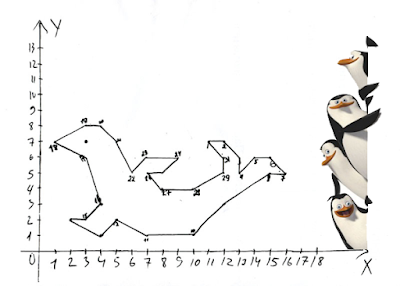
Умение работать с двоичным кодом помогло нам нарисовать такого вот морского котика:

Подробнее познакомиться с двоичной системой и переводом чисел из десятичной системы в двоичную вы можете в видео:

Система счисления – это принятый способ записи чисел и сопоставления этим записям реальных значений. Все системы счисления можно разделить на два класса:

·         позиционные – количественное значение каждой цифры зависит от ее место положения (позиции) в числе;

·         непозиционные – цифры не меняют своего количественного значения при изменении их положения в числе.

Для записи чисел в различных системах счисления используется определенное количество знаков или цифр. Число таких знаков в позиционной системе счисления называется основанием системы счисления.

Основание	Название системы счисления	Знаки
2	Двоичная	0, 1
3	Троичная	0, 1, 2
4	Четверичная	0, 1, 2, 3
5	Пятиричная	0, 1, 2, 3, 4
8	Восьмиричная	0, 1, 2, 3, 4, 5, 6, 7
10	Десятичная	0, 1, 2, 3, 4, 5, 6, 7, 8, 9
12	Двенадцатиричная	0, 1, 2, 3, 4, 5, 6, 7, 8, 9, А, В
16	Шестнадцатиричная	0, 1, 2, 3, 4, 5, 6, 7, 8, 9, А, В, C, D, E, F

Каждое число в позиционной системе счисления можно представить в виде суммы произведений коэффициентов на степени основания системы счисления.

Например:

(степени расставляем над целой частью числа слева направо, начиная с «0»)

Двоичная система счисления имеет особую значимость в информатике. Это определяется тем, что внутреннее представление любой информации в компьютере является двоичным, т. е. описываемым наборами только из двух знаков (0, 1).

Рассмотрим алгоритмы перевода числа из десятичной системы счисления в двоичную и наоборот:

Проверяйте себя!

• четные числа в двоичной форме всегда заканчиваются на 0, а нечетные - на 1;

• двоичное число не может начинаться с нуля.