Анализ линий тренда. Коэффициент регрессии

Результаты практической работы "Регрессионные модели":

Фамилия, имя	Оценка
Воронина, Машир	11
Скороход, Лижанкова	9
Мельник, Белов	11
Пюрко, Пономаренко	9
Попович, Пилипенко	10
Зацаренко, Хотинь	10
Замякин, Гусак	9
Динец, Луценко	7
Якимец, Рабковская	9
Игнатьева, Галайда, Панченко	11
Хохлов, Поставной	9

Загрузите рабочую книгу "Регрессионные модели" и скачайте себе копию.

Что такое аппроксимация?

На практике при моделировании различных процессов - в частности, экономических, физических, технических, социальных - широко используются те или иные способы вычисления приближенных значений функций по известным их значениям в некоторых фиксированных точках.

 Такого рода задачи приближения функций часто возникают:

• при построении приближенных формул для вычисления значений характерных величин исследуемого процесса по табличным данным, полученным в результате эксперимента;
• при численном интегрировании, дифференцировании, решении дифференциальных уравнений и т. д.;
• при необходимости вычисления значений функций в промежуточных точках рассматриваемого интервала;
• при определении значений характерных величин процесса за пределами рассматриваемого интервала, в частности при прогнозировании.

Если для моделирования некоторого процесса, заданного таблицей, построить функцию, приближенно описывающую данный процесс на основе метода наименьших квадратов, она будет называться аппроксимирующей функцией (регрессией), а сама задача построения аппроксимирующих функций - задачей аппроксимации.

Что такое линия тренда?

Линии тренда позволяют наглядно показать тенденции изменения данных и помогают анализировать задачи прогноза. Такого типа анализ также называется регрессионный анализ. 

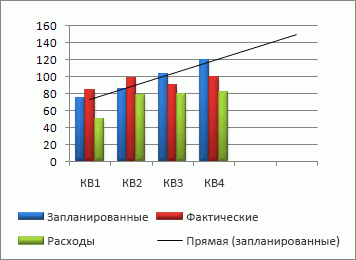
С помощью регрессионного анализа можно продолжить линию тренда на диаграмме, чтобы оценить значения, которые находятся за пределами фактических данных. Так, на приведенной ниже диаграмме простая прямая линия тренда позволяет спрогнозировать четкую тенденцию к увеличению доходов в течение двух следующих кварталов.

Выбор верного типа линии тренда для данных

При. добавлении линии тренда на диаграмму  Excel можно выбрать любой из следующих шести различных типов тренда или регрессии: 

• прямые,
• логарифмические, 
• полиномиальные, 
• степенные
• экспоненциальные
• с линейной фильтрацией. 

Тип линии тренда, который следует выбирать, определяется типом имеющихся данных.

Линия тренда получается наиболее точной, когда ее величина достоверности аппроксимации близка к единице. При аппроксимации данных с помощью линии тренда значение величины достоверности аппроксимации рассчитывается приложением Excel автоматически. При необходимости полученный результат можно показать на диаграмме.

Прямые линии тренда

Прямая линия тренда наилучшим образом описывает простой линейный набор данных. Она применяется в случаях, когда точки данных расположены близко к прямой. Иначе говоря, прямая линия тренда хорошо подходит для величины, которая возрастает или убывает с постоянной скоростью.

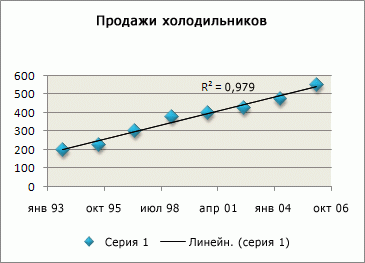
В этом примере прямая линия тренда описывает стабильный рост продаж холодильников на протяжении 13 лет. Обратите внимание, что величина достоверности аппроксимации равна 0,979, что свидетельствует о хорошем совпадении расчетной линии с данными.

Логарифмические линии тренда

Логарифмическая линия тренда хорошо описывает величину, которая вначале быстро растет или убывает, а затем постепенно стабилизируется. Логарифмическая линия тренда может использоваться как для отрицательных, так и для положительных значений данных.

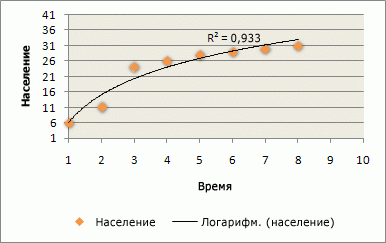
В следующем примере логарифмическая линия тренда описывает прогнозируемый рост популяции животных, обитающих в ареале с фиксированными границами. Скорость роста популяции падает из-за ограниченности жизненного пространства для животных. Кривая довольно хорошо описывает данные: величина достоверности аппроксимации равна 0,933.

Полиномиальные линии тренда

Полиномиальная линия тренда используется для описания величин, попеременно возрастающих и убывающих. Она полезна, например, для анализа большого набора данных о нестабильной величине. Степень полинома определяется количеством экстремумов (максимумов и минимумов) кривой. Полином второй степени может описать только один максимум или минимум. Полином третьей степени имеет один или два экстремума. Полином четвертой степени может иметь не более трех максимумов или минимумов.

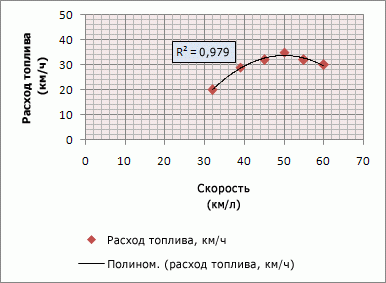
В следующем примере полиномиальная линия тренда второй степени (один максимум) описывает зависимость расхода топлива от скорости движения. Близкая к единице величина достоверности аппроксимации (0,979) свидетельствует о хорошем совпадении кривой с данными.

Степенные линии тренда

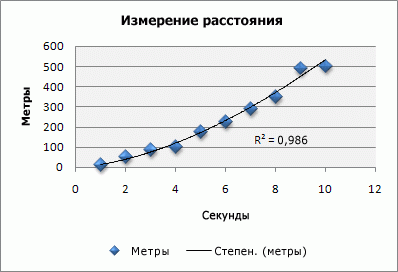
Степенная аппроксимация полезна для описания монотонно возрастающей либо монотонно убывающей величины, например расстояния, пройденного разгоняющимся автомобилем. Использование степенной аппроксимации невозможно, если данные содержат нулевые или отрицательные значения.

В следующем примере показана зависимость пройденного разгоняющимся автомобилем расстояния от времени. Расстояние выражено в метрах, время — в секундах. Эти данные точно описываются степенной линией тренда, о чем свидетельствует величина достоверности аппроксимации, равная 0,986.

Экспоненциальные линии тренда

Экспоненциальную линию тренда следует использовать в том случае, если скорость изменения данных непрерывно возрастает. Однако для данных, которые содержат нулевые или отрицательные значения, этот тип линии тренда неприменим.

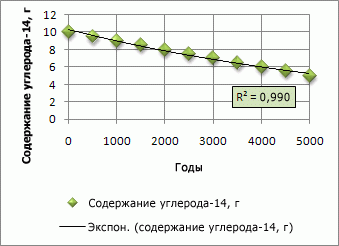
В следующем примере экспоненциальная линия тренда описывает содержание радиоактивного углерода-14 в зависимости от возраста органического объекта. Величина достоверности аппроксимации равна 0,990, что означает очень хорошее соответствие кривой данным.

Линии тренда с линейной фильтрацией

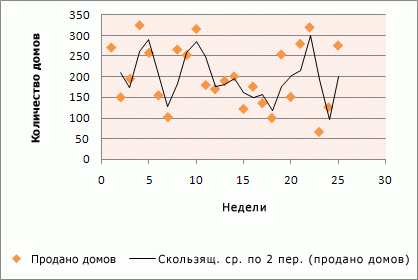
Использование линии тренда с линейной фильтрацией позволяет сгладить колебания данных и таким образом более наглядно показать характер зависимости. Линейный фильтр строится по определенному числу точек данных (оно задается параметром Точки). Элементы данных усредняются, и полученный результат используется в качестве точки линии тренда. Так, если параметр Точки равен 2, первая точка линии тренда с линейной фильтрацией определяется как среднее значение первых двух элементов данных, вторая точка — как среднее второго и третьего элементов, и так далее.

В следующем примере показана зависимость числа продаж на протяжении 26 недель, полученная путем расчета скользящего среднего.

Добавление линии тренда

На диаграмме без накопления, плоской диаграмме, диаграмме с областями, линейчатой диаграмме, гистограмме, графике, биржевой, точечной или пузырьковой диаграмме щелкните ряд данных, для которого требуется добавить линию тренда или линейную фильтрацию, или выполните указанные ниже действия, чтобы выбрать ряд данных из списка элементов диаграммы.

1. Щелкните диаграмму.
2. Будут отображены средства Работа с диаграммами, включающие вкладки Конструктор, Макет и Формат.
3. На вкладке Макет в группе Анализ выберите пункт Линия тренда.
   

Выполните одно из указанных ниже действий.

1. Выберите подходящий предопределенный параметр линии тренда.
   ПРИМЕЧАНИЕ : Линия тренда будет применена без возможности выбора конкретных параметров.
2. Нажмите Дополнительные параметры линии тренда, а затем в категории Параметры линии тренда в разделе Построение линии тренда (аппроксимация и сглаживание) выберите нужный тип линии тренда.

Если выбран тип Полиномиальная, введите в поле Степень наибольшую степень для независимой переменной.

Если выбран тип Линейная фильтрация, введите в поле Точки число точек, используемых для расчета линейного фильтра.

Если линейная фильтрация добавляется к точечной диаграмме, она базируется на порядке расположения значений X в диаграмме. Для получения нужного результата перед добавлением линейной фильтрации, возможно, потребуется отсортировать значения X.

Если линия тренда добавляется к графику, гистограмме, диаграмме с областями или линейчатой диаграмме, она вычисляется согласно допущению, что значения X равны 1, 2, 3, 4, 5, 6 и т. д. Такое допущение делается независимо от того, являются ли значения по оси X числовыми или текстовыми. Чтобы вычислить линию тренда на основе числовых значений X, необходимо использовать точечную диаграмму.

Задание дополнительных параметров линии тренда

На диаграмме без накопления, плоской диаграмме, диаграмме с областями, линейчатой диаграмме, гистограмме, графике, биржевой, точечной или пузырьковой диаграмме щелкните линию тренда, которую необходимо изменить, или выполните следующие действия, чтобы выбрать ее из списка элементов диаграммы.

1. Щелкните диаграмму.
2. Будут отображены средства Работа с диаграммами, включающие вкладки Конструктор, Макет и Формат.
3. На вкладке Макет в группе Анализ выберите пункт Линия тренда, а затем нажмите Дополнительные параметры линии тренда.
4. Чтобы указать число периодов для включения в прогноз, в разделе Прогноз укажите число периодов в поле вперед на или назад на.
5. Чтобы показать на диаграмме уравнение линии тренда, установите флажок Показывать уравнение на диаграмме.
6. На вкладке Параметры линии тренда установите флажок Поместить на диаграмму величину достоверности аппроксимации (R^2).

Моделирование случайных процессов

Как связаны теория вероятностей и азартные игры?

Теория вероятностей как математическая наука сформировалась на основе изучения азартных игр. Эти игры с незапамятных времен создавались рядом поколений именно так, чтобы в них исход опыта был независим от поддающихся наблюдению условий опыта, был чисто случайным. Самое слово «азарт» (фр. «le hazard») означает «случай». 

В пылу азарта игрок не способен здраво оценить свои шансы на выигрыш

Схемы азартных игр дают исключительные по простоте и прозрачности модели случайных явлений, позволяющие в наиболее отчетливой форме наблюдать и изучать управляющие ими специфические законы; а возможность неограниченно повторять один и тот же опыт обеспечивает экспериментальную проверку этих законов в условиях действительной массовости явлений.

Опыты Якова Бернулли

Крупный шаг вперед в развитии теории вероятностей связан с работами Якова Бернулли (1654 - 1705). Ему принадлежит первое доказательство одного из важнейших положений теории вероятностей – так называемого закона больших чисел.

Якоб Бернулли

Еще до Якова Бернулли многие отмечали как эмпирический факт ту особенность случайных явлений, которую можно назвать «свойством устойчивости частот при большом числе опытов». Было неоднократно отмечено, что при большом числе опытов, исход каждого из которых является случайным, относительная частота появления каждого данного исхода имеет тенденцию стабилизироваться, приближаясь к некоторому определенному числу – вероятности этого исхода.

Например, если много раз бросать монету, относительная частота появления герба приближается к ½; при многократном бросании игральной кости частота появления грани с пятью очками приближается к 1/6 и т.д. Яков Бернулли впервые дал теоретическое обоснование этому эмпирическому факту.

Теорема Якова Бернулли – простейшая форма закона больших чисел – устанавливает связь между вероятностью события и частотой его появления; при достаточно большом числе опытов модно с практической достоверностью ожидать сколь угодно близкого совпадения частоты с вероятностью.

Что такое случайное событие?  

Событие называется случайным, если при одних и тех же условиях оно может как произойти, так и не произойти. 

Элементарным исходом называется один из взаимоисключающих друг друга вариантов, которыми может завершиться случайный эксперимент.

Элементарным событием называется исход, неделимый на более мелкие исходы.

Свойства случайных событий

• несовместные события, т.е. появление одного из событий в единичном испытании исключает появление другого события в этом же испытании;
• единственно возможные события - при рассмотрении группы этих событий не может произойти никакое другое событие, не входящее в эту группу;
• равновозможные события, т.е. ни у одного из событий нет каких-либо преимуществ перед другими.

Классическое определение вероятности

Вероятностью случайного события А называется отношение числа благоприятных исходов m к общему числу несовместных единственно возможных и равновозможных исходов n.

Р(А) =  m / n

Функции Excel, которые мы будем использовать для моделирования случайных процессов:

Функция	Русское название	Категория	Результат работы
RAND()	СЛЧИС()	Математические	Дает случайное число в диапазоне от 0 до 1
RANDBETWEEN()	СЛУЧМЕЖДУ()	Математические	Дает случайное целое число в диапазоне от верхней до нижней границы
IF()	ЕСЛИ()	Логические	Дает одно из двух вариантов значений в зависимости от того, выполняется или нет заданное условие

Аргументы функции IF():

Аргументы	Значения
Лог_выражение	Равенство или неравенство, принимающее значение TRUE или FALSE
Значение_если_истина	Значение, которое примет функция, если ЛОГ_ВЫРАЖЕНИЕ примет значение ИСТИНА
Значение_если ложь	Значение, которое примет функция, если ЛОГ_ВЫРАЖЕНИЕ примет значение ЛОЖЬ

Откройте рабочую книгу "Случайные процессы" и загрузите себе копию.

Японське економічне диво. Інтегрований урок з географії та історії

Домашнє завдання:

Документи і матеріали

Read more publications on Calaméo

Презентація до уроку "Японія між двома війнами:

Японія

Read more publications on Calaméo

Мапа світу

Хронологія подій, що відбулися в Японії, починаючи з XVI ст. і до кінця Другої світової війни 

Закон про вибори депутатів до нижньої палати парламенту. 29 березня 1925 р. (Витяг)

 

З меморандуму Танаки Гіїті: "Позитивна політика в Маньчжурії та Монголії". 25 липня 1927 р.

Реформи в Японії

 

Презентація до уроку "Японія між двома війнами:

Японія

Read more publications on Calaméo

Підсумок уроку 

Логин: lja2010k@gmail.com
Пароль: student2017

 

Домашнє завдання з історії:

Запитання і завдання

Read more publications on Calaméo

Анализ статистических данных в Excel. Нормальное распределение

Результаты практической работы "Нормальное распределение":

Фамилия, имя	Оценка
Воронина, Машир	11
Мельник, Пюрко	9
Шкуренко, Лижанкова	10
Вакуленко, Белов	9
Пономаренко, Алексеева	8
Попович, Пилипенко	9
Луценко, Поставной	9
Игнатьева, Якимец	8
Хохлов, Гаража	9
Гусак, Замякин	8

Как можно найти закономерность в случайности?

Оказывается, даже случайные величины подчиняются законам статистики. Если выйти на улицу любого города и случайным образом выбранных прохожих спросить о том, какой у них рост, вес, возраст, доход, и т.п., а потом построить график любой из этих величин, например, роста, то мы получим случайные данные.

Отсортируем всех людей по группам, так чтобы каждый попал в свой диапазон роста, например, "от 180 до 181 включительно". 

Подсчитаем количество людей в каждой подгруппе-диапазоне, это будет частота попадания роста жителей города в этот диапазон.

Эти частоты построим по оси Y, а диапазоны отложим по оси X, в результате получим  гистограмму:

Если вам попалось достаточно много жителей, то ваша схема будет выглядеть примерно так:

Это значит, что случайная величина подчиняется нормальному закону распределения. Эту функцию называют в шутку «колоколом» или «удавом, проглотившим слона».

Если вдруг увидите термин «колоколообразная кривая», знайте, что речь идет о нормальном распределении.

Как видно, у графика имеется «горб» в середине и резкое снижение плотности по краям. В этом заключается суть нормального распределения. Другими словами, вероятность того, что случайная величина окажется около центра гораздо выше, чем то, что она сильно отклонится от середины. Смотрим на картинку:

Как анализировать нормально распределенные данные?

Теперь посмотрим на формулу, по которой нарисована колоколообразная кривая, т.е. на функцию Гаусса:

Выглядит немного пугающе, но сейчас разберемся. В функции плотности нормального распределения присутствуют: 

• π – соотношение длины окружности и его диаметра, равно примерно 3,142;
• е – основание натурального логарифма, равно примерно 2,718;
• два параметра, которые задают форму конкретной кривой
• m - математическое ожидание (в различных источниках могут использоваться другие обозначения, например, µ или a);
• σ2 - дисперсия;
• ну и сама переменная x, для которой высчитывается значение функции, т.е. плотность вероятности.

Константы, понятное дело, не меняются. Зато параметры - это то, что придает окончательный вид конкретному нормальному распределению. 

Итак, конкретная форма нормального распределения зависит от 2-х параметров: математического ожидания (m) и дисперсии (σ2). Кратко обозначается N(m, σ2) или N(m, σ). Параметр m (матожидание) определяет центр распределения, которому соответствует максимальная высота графика. Дисперсия σ2 характеризует размах вариации, то есть «размазанность» данных.

Параметр математического ожидания смещает центр распределения вправо или влево, не влияя на саму форму кривой плотности, что хорошо видно на самодвижущейся картинке:

А вот дисперсия определяет остроконечность кривой. Когда данные имеют малый разброс, то вся их масса сконцентрирована у центра. Если же у данных большой разброс, то они «размажутся» по широкому диапазону.

Статистические функции, которые понадобятся вам в работе:

Функция	Русское название	Что делает
AVERAGE()	СРЗНАЧ()	Находит среднее значение по выборке
COUNT()	СЧЕТ()	Подсчитывает число непустых ячеек в диапазоне
STDEVA()	СТАНДАРТОТКЛА()	Находит стандартное отклонение в выборке
COUNTIF()	СЧЕТЕСЛИ()	Подсчитывает число ячеек в выборке, удовлетворяющих заданному условию

Откройте рабочую книгу "Нормальное распределение" и загрузите копию.

Создание документов слияния

Результаты практической работы "Документы слияния":

Фамилия, имя	Оценка
Машир, Воронина	11
Шкуренко, Крячик	9
Попович, Пилипенко	11
Пюрко	10
Мельник, Лижанкова	11
Вакуленко, Белов	???
Алексеева, Пономаренко	10
Якимец, Рабковская	11
Поставной, Литвишко	10
Гаража, Хохлов	9
Галайда, Игнатьева	11
Гусак, Замякин	10
Луценко, Динец	10

Вашей задачей будет подготовить к печати письма для клиентов туристической фирмы. Образец письма:

Источник данных о клиентах:

Результатом работы должны быть письма для всех клиентов, подготовленные к печати.

Что такое слияние документов?

Слияние используется для создания нескольких документов одновременно. В этих документах одинаковые макет, форматирование, текст и графика. Различаются и индивидуально настраиваются только определенные разделы каждого документа. С помощью слияния в Word можно создавать такие документы, как наклейки, письма, конверты и сообщения электронной почты. В процессе слияния участвуют три документа:

• основной документ;
• источник данных;
• объединенный документ.

При связывании документа со списком рассылки вы можете добавить поля слияния, чтобы персонализировать содержимое. Поля слияния соответствуют заголовкам столбцов в списке рассылки, также называемом источником данных. В примере ниже показано, как поля из списка рассылки в Excel отображаются в документе слияния.

Вставленное поле слияния извлекает данные из списка рассылки и добавляет их в каждый конверт, сообщение, наклейку или письмо. 

Этап 1. Подготовка данных в Excel для слияния

Настройка и подготовка данных — самый важный этап процесса слияния. Электронная таблица Excel станет источником данных для списка получателей.

Ниже приведены некоторые советы по подготовке данных для слияния. Проверьте следующее:

• Названия столбцов в электронной таблице должны соответствовать именам полей, которые нужно вставить при слиянии. Например, чтобы обращаться к читателям по именам в документе, потребуются отдельные столбцы для имен и фамилий.
• Все данные, участвующие в слиянии, должны находиться на первом листе электронной таблицы.
• Записи данных, содержащие значения в процентах, денежные значения и почтовые индексы, в электронной таблице должны быть надлежащим образом отформатированы, чтобы приложение Word правильно их прочитало.
• Электронная таблица Excel, которая будет использоваться в слиянии, должна храниться на локальном компьютере.
• Изменения и дополнения необходимо внести в электронную таблицу до ее подключения к документу для слияния в Word.

Этап 2. Запуск слияния

В Word выберите Файл > Создать > Новый документ.

На вкладке Рассылки в группе Начало слияния нажмите кнопку Начать слияние и выберите нужный тип слияния.

Нажмите кнопку Выбрать получателей и выберите вариант Использовать существующий список.

Перейдите к своей электронной таблице Excel и нажмите кнопку Открыть.

Если Word предложит, выберите Лист1$ > ОК. Теперь электронная таблица Excel подключена к документу слияния, который вы создаете в Word.

Этап 3. Вставка поля слияния

Вы можете вставить одно или несколько полей слияния, которые берут данные из электронной таблицы и помещают в документ.

Вставка блока адресов для конверта, наклейки, почтового сообщения или письма

На вкладке Рассылки в группе Составление документа и вставка полей нажмите кнопку Блок адреса.

В диалоговом окне Вставка блока адреса выберите формат имени получателей для конвертов.

Нажмите кнопку ОК. В меню Файл выберите команду Сохранить.

Вставка строки приветствия в почтовое сообщение или письмо

На вкладке Рассылки в группе Составление документа и вставка полей нажмите кнопку Строка приветствия.

В диалоговом окне Вставка строки приветствия сделайте следующее:

• В разделе Формат строки приветствия измените приветствие, если нужно. Для этого выберите приветствие (по умолчанию: Уважаемый), формат имени получателя и конечный знак препинания (по умолчанию: запятая).
• В разделе Строка приветствия для неправильно заданных имен получателей выберите один из вариантов.
• Нажмите кнопку ОК.
• В меню Файл выберите команду Сохранить.

Вставка данных из электронной таблицы в почтовое сообщение или письмо

На вкладке Рассылки в группе Составление документа и вставка полей нажмите кнопку Вставить поле слияния.

В диалоговом окне Вставка поля слияния в разделе Поля выберите имя поля (имя столбца в таблице) и нажмите кнопку Вставить.

При необходимости повторите действия этапа 2, а по окончании нажмите кнопку Закрыть.

В меню Файл выберите команду Сохранить.

Этап 4. Предварительный просмотр и завершение слияния

Вставив нужные поля слияния, просмотрите результаты и убедитесь, что содержимое в порядке, после чего можно завершить процесс слияния.

На вкладке Рассылки нажмите кнопку Просмотреть результаты.

Перемещаясь по записям в источнике данных с помощью кнопок Следующая запись   и Предыдущая запись, посмотрите, как записи будут отображаться в документе.

В группе Завершение нажмите кнопку Найти и объединить и выберите вариант Печать документов или Отправить электронные сообщения.

Этап 5. Сохранение слияния

При сохранении документа слияния подключение к источнику данных сохраняется. Вы можете повторно использовать документ слияния для следующей массовой рассылки.

Откройте документ слияния и нажмите кнопку Да, когда Word спросит, нужно ли сохранить подключение.